Overview
The project focuses on using the Particle Swarm Optimization (PSO) algorithm, to solve the Traveling Salesman Problem (TSP). The generated best route is then used as a trajectory for a quadrotor to explore the given environment.
The motivation behind this project is to show that exhaustive exploration of a given environment is possible by correctly sampling waypoints in the environment. These waypoints can then be transformed into a desired optimal trajectory for tasks like mapping, search and feature tracking using quadrotors.
The generated trajectories have been tested in simulation on the CrazyFlie 2.1 quadrotors. Currently, I am developing scripts to deploy these trajectories on real CrazyFlies, using a motion capture system.
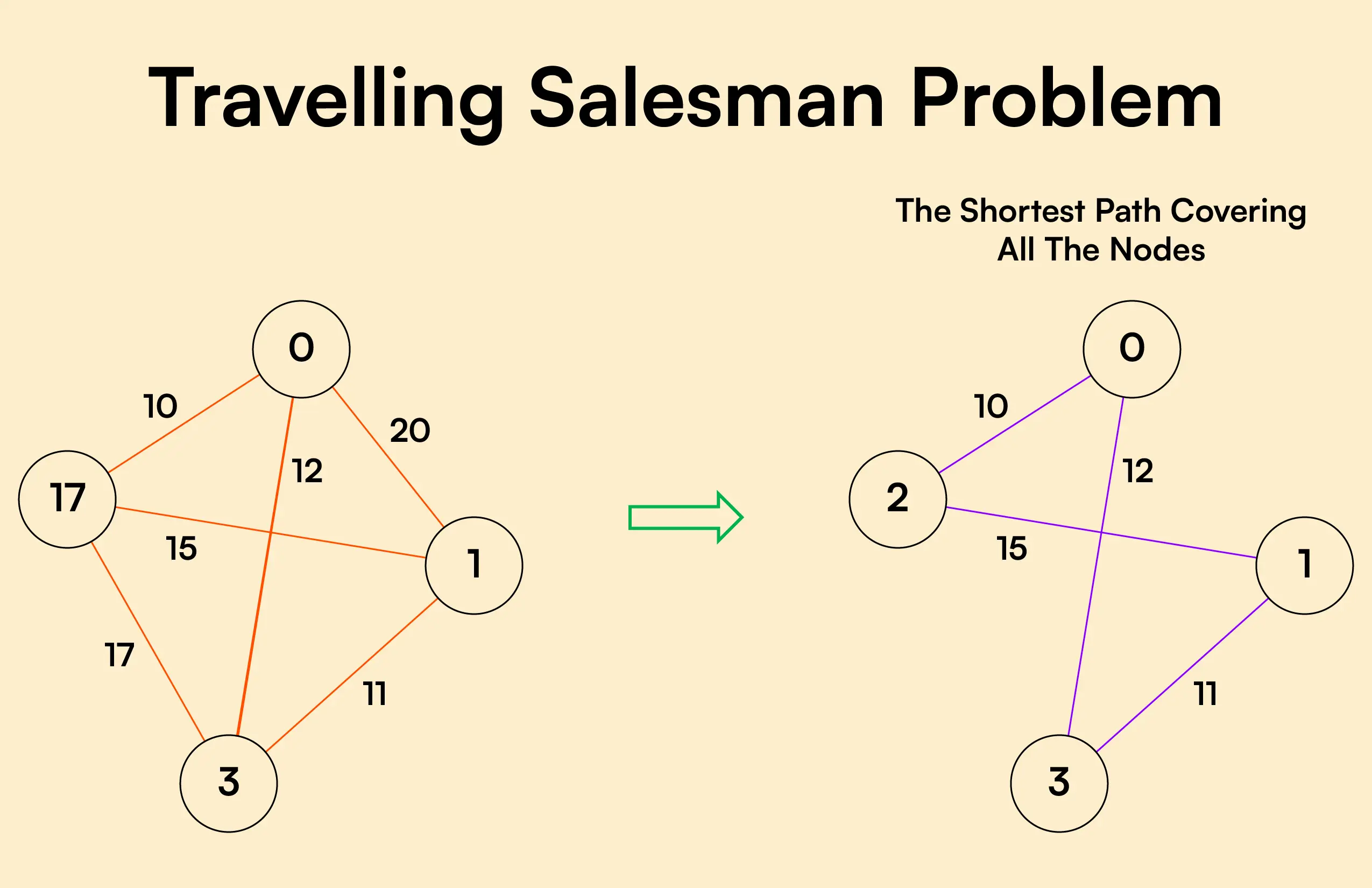
Traveling Salesman Problem
The Traveling Salesman Problem is a classic optimization challenge where the goal is to find the shortest possible route that visits a set of locations exactly once and returns to the starting point. While the problem sounds simple, it becomes incredibly complex as the number of locations grow, making it computationally expensive to solve using traditional methods. The simplest solution would be to try all permutations and see which one is cheapets. The running time for this approach lies within a polynomial factor of \(O(n!)\), the factorial of the number of cities, so this solution becomes impractical even for only 20 cities.
Using Particle Swarm Optimization (PSO), we can iteratively refine the solution to the Traveling Salesman Problem, converging to an approximate yet highly effective route.
Particle Swarm Optimization
Particle Swarm Optimization is a bio-inspired optimization algorithm that mimics the collective behavior of swarms, such as birds flocking or fish schooling, to solve complex problems. The algorithm works by iteratively improving a set of candidate solutions (called particles) based on their own best-known position and the best-known position of the entire swarm.
The PSO algorithm updates the velocity and position of each particle using the following equations: $$v_i(t+1) = w * v_i(t) + c_1 * r_1 * (p_{best_i} - x_i(t)) + c_2 * r_2 * (g_{best} - x_i(t))$$ $$x_i(t+1) = x_i(t) + v_i(t+1)$$
- \(v_i(t)\) : velocity of particle \(i\) at iteration \(t\) \
- \(x_i(t)\) : position of particle \(i\) at iteration \(t\) \
- \(w\) : inertia weight\
- \(c_1\), \(c_2\) : acceleration coefficients\
- \(r_1\),\(r_2\) : random numbers between 0 and 1\
- \(p_{best_i}\) : personal best position of particle \(i\)\
- \(g_{best}\) : global best position among all particles
The PSO algorithm initializes a population of particles, each representing a potential solution. Each particle has a position \(x_i\) and a velocity \(v_i\) in the search space. The position update mechanism is influenced by three components:
- Inertia Component: Maintains the particle’s direction
- Cognitive Component: Drives the particle towards its personal best position
- Social Component: Encourages movement towards the global best position
Implementation
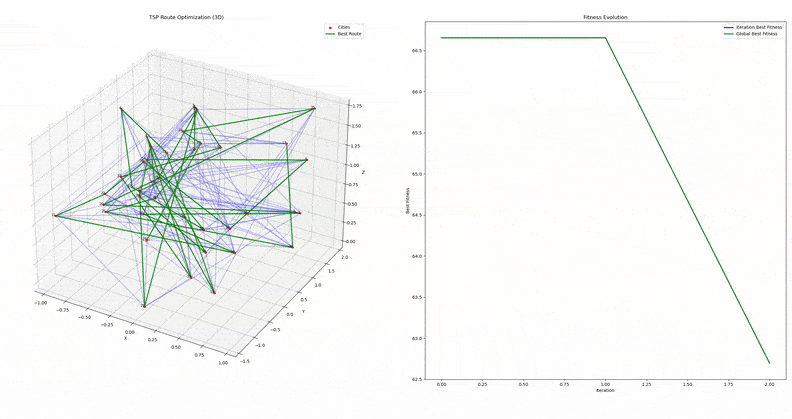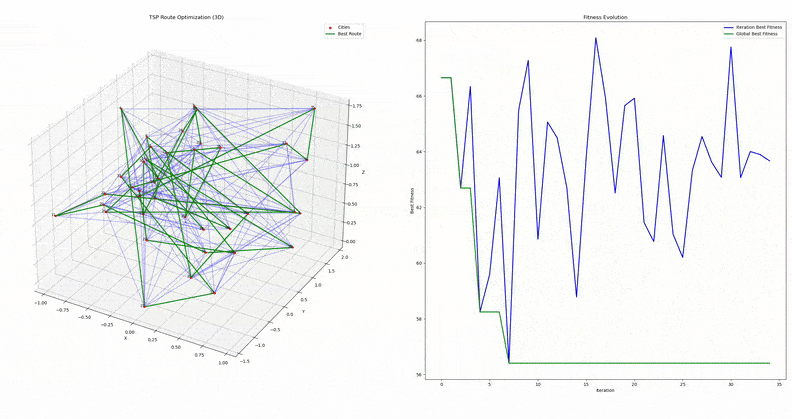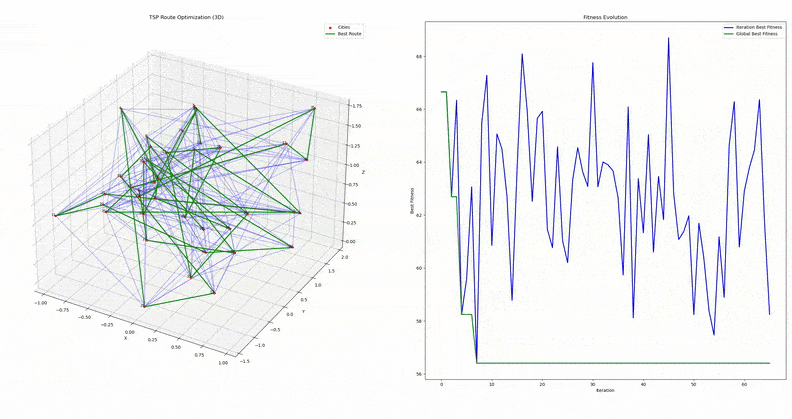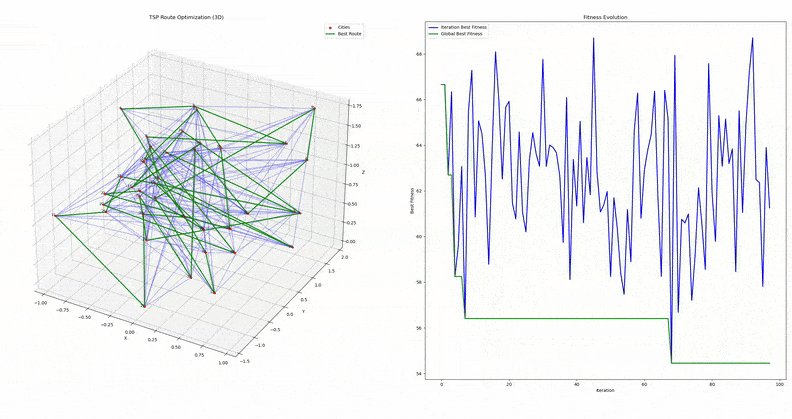
My implementation of PSO was done in C++ and consisted of the following steps:
- Randomly initialize a set of waypoints (cities) in a given search space with known bounds
- Initialize the set of particles with a random route, and calculate the fitness values of these routes
- Update the particles
- The velocity update follows the standard PSO equation, but the position update uses the velocity vector to calculate a swap index
- If the magnitude of velcoity at a particular index is high, the corresponding city in the route is more likely to be swapped with another city
- Validate the route to ensure it remains a valid permutation of the cities
- Update global best route and fitness values
- Terminate the algorithm after a set number of iterations are completed
- Convert the output waypoints into a quadrotor trajectory using this uav-trajectories
Acknowledgements
This project was a part of the course ME495: Advanced Programming Concepts in C++ at Northwestern University. Thank you to Grayson Snyder for collaborating with me on this project.